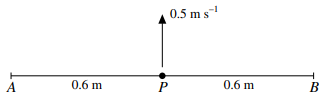
A light elastic string of natural length $1.2{\text{ }}m$ and modulus of elasticity $24{\text{ }}N$ is attached to fixed points $A$ and $B$ on a smooth horizontal surface, where $AB = 1.2{\text{ }}m$. A particle $P$ is attached to the mid-point of the string. $P$ is projected with speed $0.5{\text{ }}m{\text{ }}{s^{ - 1}}$ along the surface in a direction perpendicular to $AB$ (see diagram). $P$ comes to instantaneous rest at a distance $0.25{\text{ }}m$ from $AB$.

a) Show that the mass of $P$ is $0.8{\text{ }}kg$.

b) Calculate the greatest deceleration of $P$.