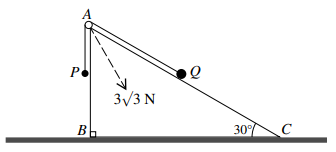
A small smooth pulley is fixed at the highest point $A$ of a cross-section $ABC$ of a triangular prism. Angle $ABC = {90^ \circ }$ and angle $BCA = {30^ \circ }$. The prism is fixed with the face containing $BC$ in contact with a horizontal surface. Particles $P$ and $Q$ are attached to opposite ends of a light inextensible string, which passes over the pulley. The particles are in equilibrium with $P$ hanging vertically below the pulley and $Q$ in contact with $AC$. The resultant force exerted on the pulley by the string is $3\surd 3{\text{ }}N$ (see diagram).

a) Show that the tension in the string is $3{\text{ }}N$.

The coefficient of friction between $Q$ and the prism is 0.75.

b) Given that $Q$ is in limiting equilibrium and on the point of moving upwards, find its mass.