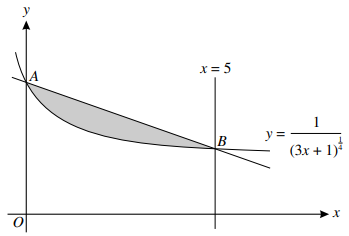
a) $A = \left( {0,{\text{ }}1} \right)$

$B = \left( {5,{\text{ }}{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}} \right)$

$y - 1 =  - \frac{1}{{10}}\left( {x - 0} \right)$

$y =  - \frac{1}{{10}}x + 1$

b) Curve: $\left( \pi  \right)\int_0^5 {{{\left( {3x + 1} \right)}^{ - 1/2}}dx} $

$\frac{{2\pi }}{3}[{\left( {3x + 1} \right)^{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}]_0^5$

$\frac{{2\pi }}{3}\left[ {4 - 1} \right]$

$\left[ {2\pi } \right]$

Line: $\left( \pi  \right)\int_0^5 {(\frac{1}{{100}}{x^2} - \frac{1}{5}x + 1)dx} $

$\left( \pi  \right)[\frac{1}{{300}}{x^3} - \frac{1}{{10}}{x^2} + x]_0^5$

$\left( \pi  \right)[\frac{{125}}{{300}} - \frac{{25}}{{10}} + 5]$

$[\frac{{35\pi }}{{12}}]$

Volume $ = \frac{{35\pi }}{{12}} - 2\pi  = \frac{{11\pi }}{{12}}$