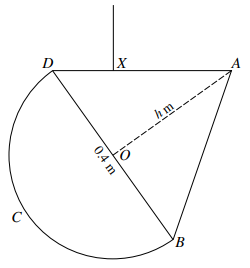
A uniform lamina $ABCD$ consists of a semicircle $BCD$ with centre $O$ and diameter $0.4{\text{ }}m$, and an isosceles triangle $ABD$ with base $BD = 0.4{\text{ }}m$ and perpendicular height $h{\text{ m}}$. The centre of mass of the lamina is at $O$.
a) Find the value of $h$.
b) The lamina is suspended from a vertical string attached to a point $X$ on the side $AD$ of the triangle (see diagram). Given the lamina is in equilibrium with $AD$ horizontal, calculate $XD$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...