Functions f and g are defined by
$f:x \mapsto 3x - 4$, $x \in \mathbb{R}$,
$g:x \mapsto 2{\left( {x - 1} \right)^3} + 8$, $x \gt 1$.
a) Evaluate $fg\left( 2 \right)$.
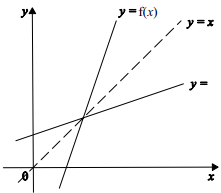
b) Sketch in a single diagram the graphs of $y = f\left( x \right)$ and $y = {f^{ - 1}}\left( x \right)$, making clear the relationship between the graphs.
c) Obtain an expression for $g\prime \left( x \right)$ and use your answer to explain why g has an inverse.
d) Express each of ${f^{ - 1}}\left( x \right)$ and ${g^{ - 1}}\left( x \right)$ in terms of $x$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...