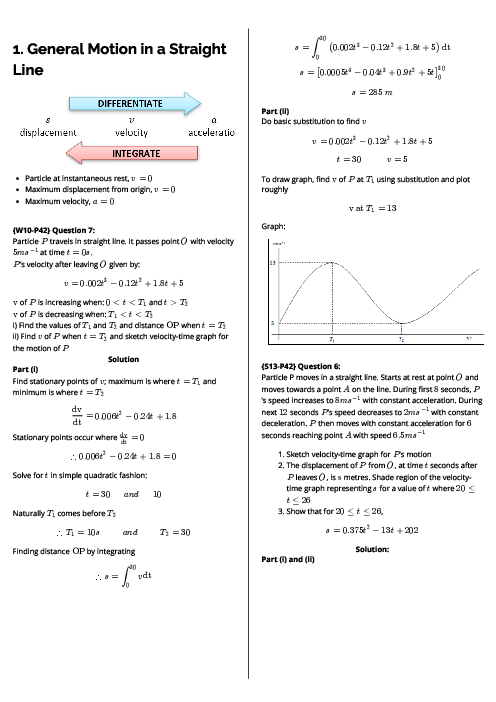
A uniform rod $AB$ of weight $16{\text{ }}N$ is freely hinged at $A$ to a fixed point. A force of magnitude $4{\text{ }}N$ acting perpendicular to the rod is applied at $B$ (see diagram). Given that the rod is in equilibrium,
a) calculate the angle the rod makes with the horizontal,
b) find the magnitude and direction of the force exerted on the rod at $A$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...