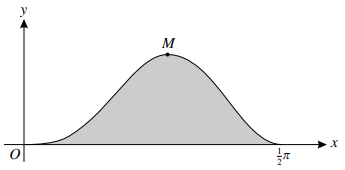
The diagram shows the curve $y = 5{\text{ }}{\sin ^3}x{\cos ^2}x$ for $0 \leqslant x \leqslant \frac{1}{2}\pi $, and its maximum point $M$.
a) Find the x-coordinate of $M$.
b) Using the substitution $u = \cos x$, find by integration the area of the shaded region bounded by the curve and the x-axis.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...