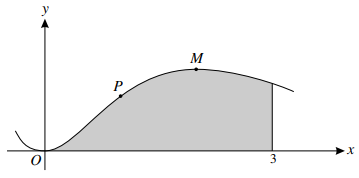
The diagram shows the curve $y = {x^2}{e^{ - x}}$.
a) Show that the area of the shaded region bounded by the curve, the x-axis and the line $x = 3$ is equal to $2 - \frac{{17}}{{{e^3}}}$.
b) Find the x-coordinate of the maximum point $M$ on the curve.
c) Find the x-coordinate of the point $P$ at which the tangent to the curve passes through the origin.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...