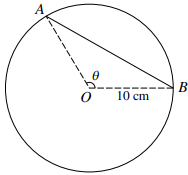
The diagram shows a circle with centre $O$ and radius $10{\text{ }}cm$. The chord $AB$ divides the circle into two regions whose areas are in the ratio 1 : 4 and it is required to find the length of $AB$. The angle $AOB$ is $\theta $ radians.
a) Show that $\theta = \frac{2}{5}\pi + \sin \theta $.
b) Showing all your working, use an iterative formula, based on the equation in part (a), with an initial value of 2.1, to find $\theta $ correct to 2 decimal places. Hence find the length of $AB$ in centimetres correct to 1 decimal place.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!











