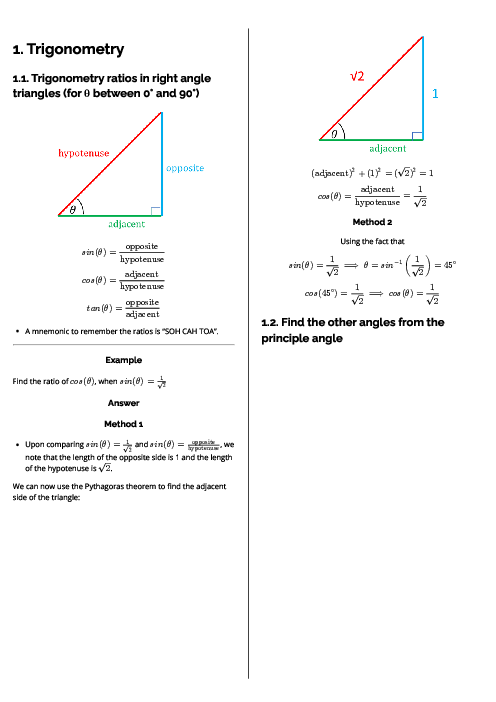
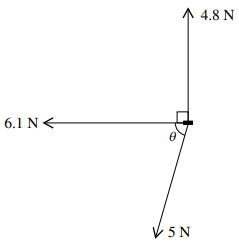
A small block of mass $1.25{\text{ }}kg$ is on a horizontal surface. Three horizontal forces, with magnitudes and directions as shown in the diagram, are applied to the block. The angle $\theta $ is such that $\cos \theta  = 0.28$ and $\sin \theta  = 0.96$. A horizontal frictional force also acts on the block, and the block is in equilibrium.

a) Show that the magnitude of the frictional force is $7.5{\text{ }}N$ and state the direction of this force.

b) Given that the block is in limiting equilibrium, find the coefficient of friction between the block and the surface.

The force of magnitude $6.1{\text{ }}N$ is now replaced by a force of magnitude $8.6{\text{ }}N$ acting in the same direction, and the block begins to move.

c) Find the magnitude and direction of the acceleration of the block.