a) Use correct product rule
Obtain correct derivative in any form
Equate derivative to zero and find non-zero $x$
Obtain $x = \exp \left( { - \frac{1}{3}} \right)$, or equivalent
Obtain $y = - 1/\left( {3e} \right)$, or any ln-free equivalent
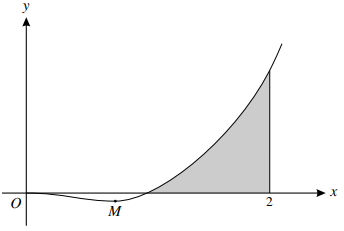
b) Integrate and reach $k{x^4}\ln x + l\int {{x^4}.\frac{1}{x}\,dx} $
Obtain $\frac{1}{4}{x^4}\ln x - \frac{1}{4}\int {{x^3}\,dx} $
Obtain integral $\frac{1}{4}{x^4}\ln x - \frac{1}{{16}}{x^4}$, or equivalent
Use limits $x = 1$ and $x = 2$ correctly, having integrated twice
Obtain answer $4ln{\text{ }}2 - \frac{{15}}{{16}}$, or exact equivalent