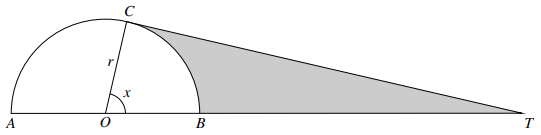
The diagram shows a semicircle $ACB$ with centre $O$ and radius $r$. The tangent at $C$ meets $AB$ produced at $T$. The angle $BOC$ is $x$ radians. The area of the shaded region is equal to the area of the semicircle.
a) Show that $x$ satisfies the equation
$\tan x = x + \pi $.
b) Use the iterative formula ${x_{n + 1}} = {\tan ^{ - 1}}\left( {{x_n} + \pi } \right)$ to determine $x$ correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...