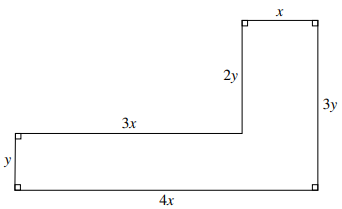
The diagram shows the dimensions in metres of an L-shaped garden. The perimeter of the garden is $48{\text{ }}m$.
a) Find an expression for $y$ in terms of $x$.
b) Given that the area of the garden is $A\,{m^2}$, show that $A = 48x - 8{x^2}$.
c) Given that $x$ can vary, find the maximum area of the garden, showing that this is a maximum value rather than a minimum value.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...