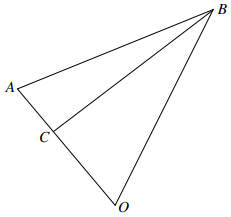
The diagram shows triangle $OAB$, in which the position vectors of $A$ and $B$ with respect to $O$ are given by
$\overrightarrow {OA} = 2i + j - 3k$ and $\overrightarrow {OB} = - 3i + 2j - 4k$.
$C$ is a point on $OA$ such that $\overrightarrow {OC} = p\,\overrightarrow {OA} $, where $p$ is a constant.
a) Find angle $AOB$.
b) Find $\overrightarrow {BC} $ in terms of p and vectors $i$, $j$ and $k$.
c) Find the value of $p$ given that $BC$ is perpendicular to $OA$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...