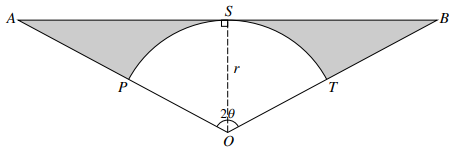
In the diagram, $OAB$ is an isosceles triangle with $OA = OB$ and angle $AOB = 2\theta $ radians. Arc $PST$ has centre $O$ and radius $r$, and the line $ASB$ is a tangent to the arc $PST$ at $S$.
a) Find the total area of the shaded regions in terms of $r$ and $\theta $.
b) In the case where $\theta = \frac{1}{3}\pi $ and $r = 6$, find the total perimeter of the shaded regions, leaving your answer in terms of $\surd 3$ and $\pi $.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!










