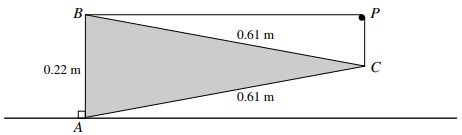
$ABC$ is a uniform triangular lamina of weight $19{\text{ N}}$, with $AB = 0.22{\text{ }}m$ and $AC = BC = 0.61{\text{ }}m$.

The plane of the lamina is vertical. $A$ rests on a rough horizontal surface, and $AB$ is vertical. The equilibrium of the lamina is maintained by a light elastic string of natural length $0.7{\text{ }}m$ which passes over a small smooth peg $P$ and is attached to $B$ and $C$. The portion of the string attached to $B$ is horizontal, and the portion of the string attached to $C$ is vertical (see diagram).

a) Show that the tension in the string is $10{\text{ }}N$.

b) Calculate the modulus of elasticity of the string. 

c) Find the magnitude and direction of the force exerted by the surface on the lamina at $A$.