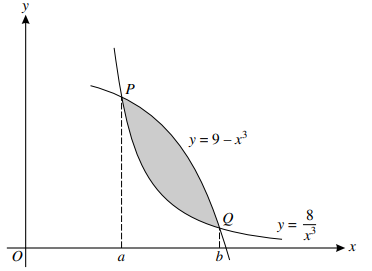
The diagram shows parts of the curves $y = 9 - {x^3}$ and $y = \frac{8}{{{x^3}}}$ and their points of intersection $P$ and $Q$. The x-coordinates of $P$ and $Q$ are $\alpha $ and $b$ respectively.
a) Show that $x = \alpha $ and $x = b$ are roots of the equation ${x^6} - 9{x^3} + 8 = 0$. Solve this equation and hence state the value of $\alpha $ and the value of $b$.
b) Find the area of the shaded region between the two curves.
c) The tangents to the two curves at $x = c$ (where $\alpha \lt c \lt b$) are parallel to each other. Find the value of $c$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...