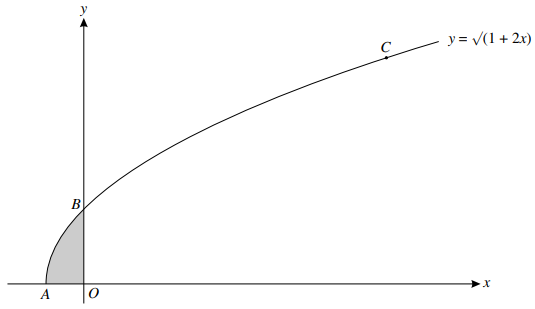
The diagram shows the curve meeting the x-axis at and the y-axis at . The y-coordinate of the point on the curve is 3. a) Find the coordinates of and . b) Find… | Mathematics (9709) AS & A Level شماره 20171

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

بنظر میرسد شما قادر به دریافت پیامکهای ما نیستید!
لطفا برای فعال سازی کد
{{ receive_code }}
را از طریق شماره
{{ identity }}
به شماره
100078000
ارسال کنید.

منتظر بمانید تا فعال سازی انجام شود!

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

قوانین و مقررات را خواندم و می پذیرم.

قبلا ثبت نام کرده اید؟ وارد شوید!

موبایل یا ایمیل

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد! )

منتظر دریافت پیامک شما ...

یه رمز خوب که یادت بمونه بزن:

ورود | ثبت نام

لطفا کمی صبر کنید ...

دوست خوبم!
برای نگهداری سابقه خریدتان، نیاز به شماره موبایل (یا ایمیل) شما داریم.

موبایل یا ایمیل

رمزعبور اگه یادت نیس نزن :)

یه کد به {{ identity }} فرستادم، لطفا بگو:

ارسال دوباره کد ( {{ countDown }} ثانیه صبر کن شاید اومد!)

منتظر دریافت پیامک شما ...

ورود با رمزعبور

گزینه انتخاب شده در پاسخنامه درست نیست.

بیش از یک گزینه درست وجود دارد.

هیچ گزینه ای درست نیست.

اشکال تایپی در صورت سوال یا در گزینه ها وجود دارد.

این تست با تست دیگری در همین آزمون تشابه دارد.

در پاسخ تشریحی اشکال وجود دارد.

این تست خارج از بودجه بندی یا مبحث مورد نظر است.

سایر موارد

حداقل 25 کاراکتر باید وارد کنید.

Paper 1: Pure Mathematics 1 Mathematics (9709) AS & A Level CIE

The diagram shows the curve $y = \surd \left( {1 + 2x} \right)$ meeting the x-axis at $A$ and the y-axis at $B$. The y-coordinate of the point $C$ on the curve is 3.

a) Find the coordinates of $B$ and $C$.

b) Find the equation of the normal to the curve at $C$.

c) Find the volume obtained when the shaded region is rotated through ${360^ \circ }$ about the y-axis.

نمایش پاسخ

a) $B = \left( {0,1} \right)$ $C = \left( {4,3} \right)$

b) $\frac{{\delta y}}{{\delta x}} = \frac{1}{2} \times 2{\left( {1 + 2x} \right)^{ - \frac{1}{2}}}$

Grad. of normal $ = - 3$

$y - 3 = - 3\left( {x - 4} \right)$ or $y = - 3x + 15{\text{ }}$ oe

c) ${y^2} = 1 + 2x \Rightarrow x = \frac{1}{{2\left( {{y^2} - 1} \right)}}\,\,\,SOI$

$\left( \pi \right) \times \frac{1}{4} \times \int {\left( {{y^4} - 2{y^2} + 1} \right)\delta y} $

$\left( \pi \right) \times \frac{1}{4}\left[ {\frac{{{y^5}}}{5} - \frac{{2{y^3}}}{3} + y} \right]$

$\left( \pi \right) \times \frac{1}{4}\left[ {\frac{1}{5} - \frac{2}{3} + 1} \right]$

$\frac{2}{{15}}\pi $

گزارش اشکال

جستجوهای پرتکرار

پاسخ تشریحی :

تحلیل ویدئویی تست

با گنجینه سوال

نمونه سوالات مشابه

اطلاع از تغییرات در بسته‌های گاما

کاربر عزیز سلام!

پاسخ تشریحی :

تحلیل ویدئویی تست

با گنجینه سوال

نمونه سوالات مشابه