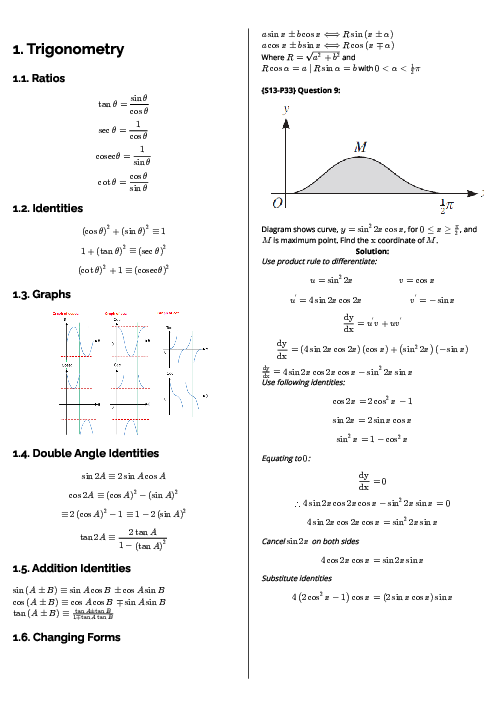
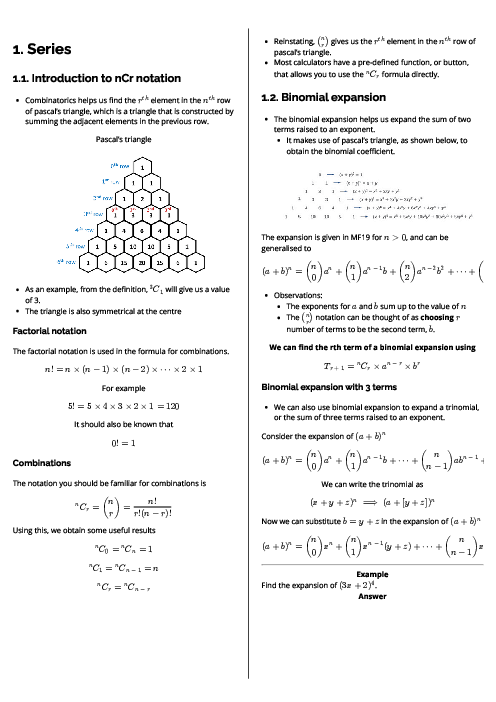
With respect to the origin $O$, the position vectors of two points $A$ and $B$ are given by $\overrightarrow {OA} = i + 2j + 2k$ and $\overrightarrow {OB} = 3i + 4j$. The point $P$ lies on the line through $A$ and $B$, and $\overrightarrow {AP} = \lambda \overrightarrow {AB} $.
a) Show that $\overrightarrow {OP} = \left( {1 + 2\lambda } \right)i + \left( {2 + 2\lambda } \right)j + \left( {2 - 2\lambda } \right)k$.
b) By equating expressions for $\cos AOP$ and $\cos BOP$ in terms of in terms of $\lambda $, find the value of $\lambda $ for which $OP$ bisects the angle $AOB$.
c) When $\lambda $ has this value, verify that $AP:PB = OA:OB$.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!