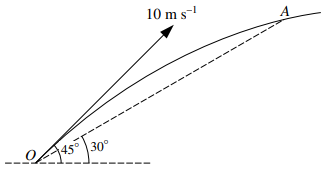
A particle $P$ is projected from a point $O$ with initial speed $10{\text{ }}m{\text{ }}{s^{ - 1}}$ at an angle of ${45^ \circ }$ above the horizontal. $P$ subsequently passes through the point $A$ which is at an angle of elevation of ${30^ \circ }$ from $O$ (see diagram). At time $t\,s$ after projection the horizontal and vertically upward displacements of $P$ from $O$ are $x$ m and $y{\text{ }}m$ respectively.
a) Write down expressions for $x$ and $y$ in terms of $t$, and hence obtain the equation of the trajectory of $P$.
b) Calculate the value of $x$ when $P$ is at $A$.
c) Find the angle the trajectory makes with the horizontal when $P$ is at $A$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...