A smooth hemispherical shell, with centre $O$, weight $12{\text{ N}}$ and radius $0.4{\text{ }}m$, rests on a horizontal plane. A particle of weight $W{\text{ N}}$ lies at rest on the inner surface of the hemisphere vertically below $O$.

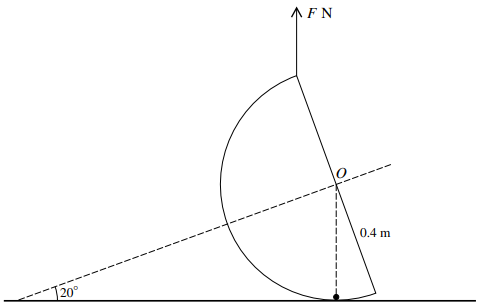
A force of magnitude $F{\text{ N}}$ acting vertically upwards is applied to the highest point of the hemisphere, which is in equilibrium with its axis of symmetry inclined at ${20^ \circ }$ to the horizontal (see diagram).

a) Show, by taking moments about $O$, that $F = 16.48$ correct to 4 significant figures.

b) Find the normal contact force exerted by the plane on the hemisphere in terms of $W$. Hence find the least possible value of $W$.