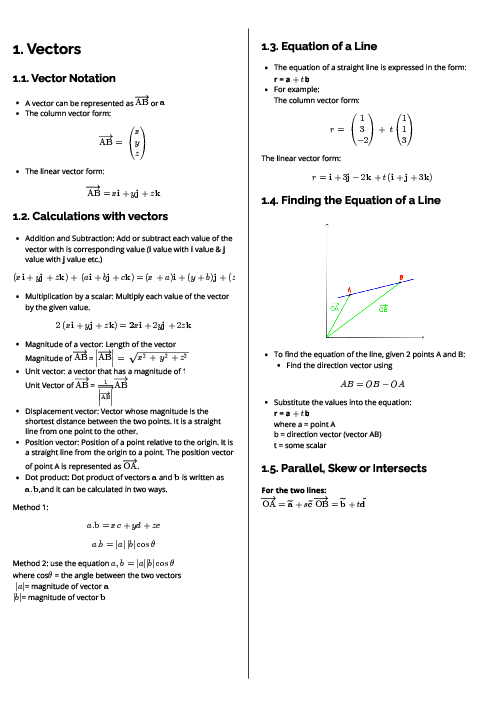
A particle travels along a straight line. It starts from rest at a point $A$ on the line and comes to rest again, 10 seconds later, at another point $B$ on the line. The velocity $t$ seconds after leaving $A$ is
$0.72{t^2} - 0.096{t^3}$ for $0 \leqslant t \leqslant 5$,
$2.4t - 0.24{t^2}$ for $5 \leqslant t \leqslant 10$
a) Show that there is no instantaneous change in the acceleration of the particle when $t = 5$.
b) Find the distance $AB$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...