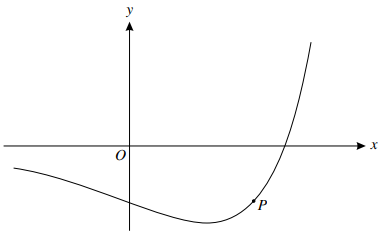
The diagram shows the curve $y = \left( {x - 4} \right){e^{\frac{1}{2}x}}$. The curve has a gradient of 3 at the point $P$.
a) Show that the x-coordinate of $P$ satisfies the equation
$x = 2 + 6{e^{ - \frac{1}{2}x}}$.
b) Verify that the equation in part (a) has a root between $x = 3.1$ and $x = 3.3$.
c) Use the iterative formula ${x_{n + 1}} = 2 + 6{e^{ - \frac{1}{2}{x_n}}}$ to determine this root correct to 2 decimal places. Give the result of each iteration to 4 decimal places.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...