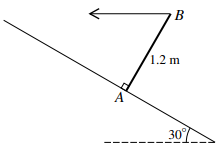
A uniform rod $AB$ has weight $15{\text{ }}N$ and length $1.2{\text{ }}m$. The end $A$ of the rod is in contact with a rough plane inclined at ${30^ \circ }$ to the horizontal, and the rod is perpendicular to the plane. The rod is held in equilibrium in this position by means of a horizontal force applied at $B$, acting in the vertical plane containing the rod (see diagram).
a) Show that the magnitude of the force applied at $B$ is $4.33{\text{ }}N$, correct to 3 significant figures.
b) Find the magnitude of the frictional force exerted by the plane on the rod.
c) Given that the rod is in limiting equilibrium, calculate the coefficient of friction between the rod and the plane.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...