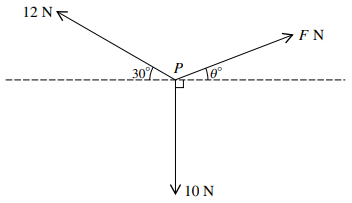
a) $F\cos \theta  = 12\cos {30^ \circ }\left( { = 10.932} \right)$

$F\sin \theta  = 10 - 12\sin {30^ \circ }\left( { = 4} \right)$

$F = 11.1$ or $\theta  = 21.1$  (accept $21.0$)

$\theta  = 21.1$ (accept $21.0$) or $F = 11.1$

b) Magnitude is $12N$

Direction is ${30^ \circ }$ clockwise from $ + ve$ ‘x’ axis

alternative for 4 (a)

For triangle of forces with sides 12, F and 10 and at least one of the angles $\left( {{{90}^ \circ } - \theta } \right)$ or ${60^ \circ }$ or $\left( {\theta  + {{30}^ \circ }} \right)$

${F^2} = {12^2} + {10^2} - 2 \times 12 \times 10\cos {60^ \circ }$ or

$\left( {12\cos {{30}^ \circ }} \right)\sin \theta  = \left( {10 - 12\sin {{30}^ \circ }} \right)\cos \theta {\text{ }}$

$F = 11.1$ or $\theta  = 21.1$ (accept $21.0$)

$\theta  = 21.1$ (accept $21.0$) or $F = 11.1$

second alternative for 4 (a)

For using Lami’s theorem with $12{\text{ }}N$ and $10{\text{ }}N$

$12/\sin \left( {90 + \theta } \right) = 10/\sin \left( {150 - \theta } \right)$

$12/\cos \theta  = 20 \div \left( {\cos \theta  + {3^{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}\sin \theta } \right)$

$ \to 12 \times {3^{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}\sin \theta  = 8\cos \theta $

$ \to \tan \theta  = 2 \div \left( {3 \times {3^{{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}}}} \right)$

$ \to \theta  = 21.1$

For using Lami’s theorem with $F{\text{ }}N$ and ($12{\text{ }}N$ or $10{\text{ }}N$)

$F/\sin {120^ \circ } = 12/\sin {111.1^ \circ }$ (or $10/\sin {128.9^ \circ }$)

$F = 11.1$

Alternative for 4 (b)

For $X = 11.1\cos {21.1^ \circ }$ and

$Y = 11.1\sin {21.1^ \circ } - 10$,

${R^2} = {X^2} + {Y^2}$ and $\tan \Phi  = Y/X$

Magnitude $12{\text{ }}N$ and direction ${30^ \circ }$ clockwise from $ + ve$ x-axis