A uniform solid cylinder has radius $0.7{\text{ }}m$ and height $h{\text{ }}m$. A uniform solid cone has base radius $0.7{\text{ }}m$ and height $2.4{\text{ }}m$. The cylinder and the cone both rest in equilibrium each with a circular face in contact with a horizontal plane. The plane is now tilted so that its inclination to the horizontal, ${\theta ^ \circ }$, is increased gradually until the cone is about to topple.

a) Find the value of $\theta $ at which the cone is about to topple.

b) Given that the cylinder does not topple, find the greatest possible value of $h$.

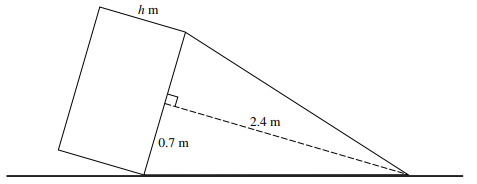
The plane is returned to a horizontal position, and the cone is fixed to one end of the cylinder so that the plane faces coincide. It is given that the weight of the cylinder is three times the weight of the cone. The curved surface of the cone is placed on the horizontal plane (see diagram).

c) Given that the solid immediately topples, find the least possible value of $h$.