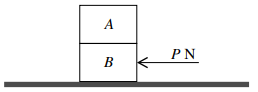
Two rectangular boxes $A$ and $B$ are of identical size. The boxes are at rest on a rough horizontal floor with $A$ on top of $B$. Box $A$ has mass $200{\text{ }}kg$ and box $B$ has mass $250{\text{ }}kg$. A horizontal force of magnitude $P{\text{ }}N$ is applied to $B$ (see diagram). The boxes remain at rest if $P \leqslant 3150$ and start to move if $P \gt 3150$.
a) Find the coefficient of friction between $B$ and the floor.
The coefficient of friction between the two boxes is 0.2. Given that $P \gt 3150$ and that no sliding takes place between the boxes,
b) show that the acceleration of the boxes is not greater than $2{\text{ }}m{\text{ }}{s^{ - 2}}$,
c) find the maximum possible value of $P$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...