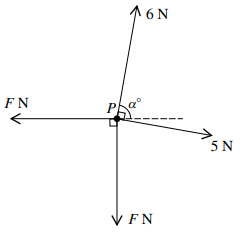
$6\cos {\alpha ^ \circ } + 5\cos \left( {{{90}^ \circ } - {\alpha ^ \circ }} \right) = F$ and

$6\sin {\alpha ^ \circ } - 5\cos \left( {{{90}^ \circ } - {\alpha ^ \circ }} \right) = F$

$[6\cos {\alpha ^ \circ } + 5\sin {\alpha ^ \circ } = 6\sin {\alpha ^ \circ } - 5\cos {\alpha ^ \circ }$

$ \to 11\cos {\alpha ^ \circ } = \sin {\alpha ^ \circ }]{\text{ }}$

$\alpha  = 84.8$

$[F = 6\cos {84.8^ \circ } + 5\sin {84.8^ \circ }{\text{ }};{\text{ }}F = 6\sin {84.8^ \circ } - $

$5\cos {84.8^ \circ }]$

$F = 5.52$

First alternative scheme

$\left[ {2{F^2} = 25 + 36} \right]$

$F = 5.52$

$\tan \left( {{\alpha ^ \circ } - {{45}^ \circ }} \right) = 5/6$ or $\tan \left( {{{135}^ \circ } - {\alpha ^ \circ }} \right) = 6/5$ or

$\cos \left( {{\alpha ^ \circ } - {{45}^ \circ }} \right)$ or $\sin \left( {{{135}^ \circ } - {\alpha ^ \circ }} \right) = 6/\sqrt {61} $ or

$\sin \left( {{\alpha ^ \circ } - {{45}^ \circ }} \right)$ or $\cos \left( {{{135}^ \circ } - {\alpha ^ \circ }} \right) = 5/\sqrt {61} $

$\alpha  = 84.8$

Second alternative scheme

$[6\cos {\alpha ^ \circ } + 5\cos \left( {{{90}^ \circ } - {\alpha ^ \circ }} \right)$

$ = 6\sin {\alpha ^ \circ } - 5\sin \left( {{{90}^ \circ } - {\alpha ^ \circ }} \right)]$

$\left[ {11\cos {\alpha ^ \circ } - \sin {\alpha ^ \circ } = 0} \right]$

$\alpha  = 84.8$

For $F = 6\cos {\alpha ^ \circ } + 5\cos \left( {{{90}^ \circ } - {\alpha ^ \circ }} \right)$ or

$F = 6\sin {\alpha ^ \circ } - 5\sin \left( {{{90}^ \circ } - {\alpha ^ \circ }} \right)$

$F = 5.52$