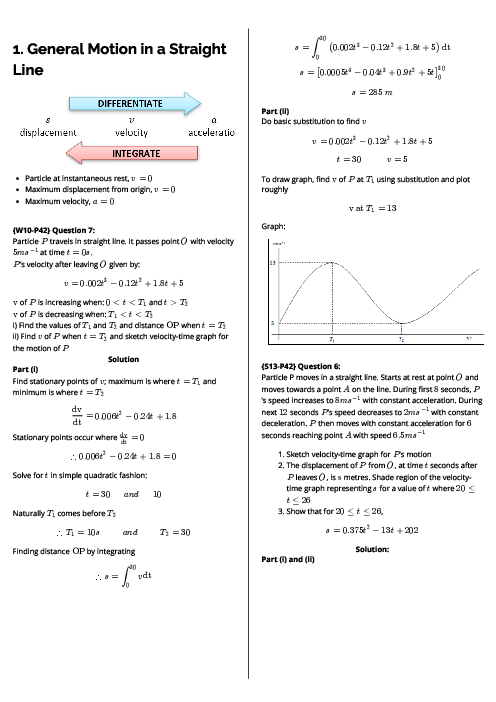
The diagram shows a quadrilateral $ABCD$ in which the point $A$ is $\left( { - 1,{\text{ }} - 1} \right)$, the point $B$ is $\left( {3,{\text{ }}6} \right)$ and the point $C$ is $\left( {9,{\text{ }}4} \right)$. The diagonals $AC$ and $BD$ intersect at $M$. Angle $BMA = {90^ \circ }$ and $BM = MD$. Calculate
a) the coordinates of $M$ and $D$,
b) the ratio $AM:MC$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...