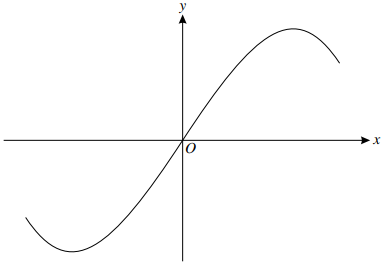
The diagram shows the curve with parametric equations
$x = \sin t + \cos t$, $y = {\sin ^3}t + {\cos ^3}t$,
for $\frac{1}{4}\pi \lt t \lt \frac{5}{4}\pi $.
a) Show that $\frac{{dy}}{{dx}} = - 3\sin t\cos t$.
b) Find the gradient of the curve at the origin.
c) Find the values of $t$ for which the gradient of the curve is 1, giving your answers correct to 2 significant figures.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...