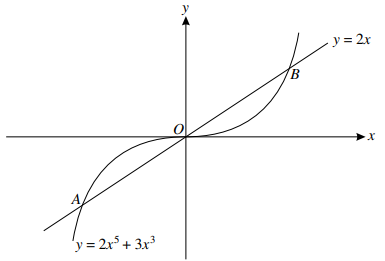
The diagram shows the curve $y = 2{x^5} + 3{x^3}$ and the line $y = 2x$ intersecting at points $A$, $O$ and $B$.
a) Show that the x-coordinate of $A$ and $B$ satisfy the equation $2{x^4} + 3{x^2} - 2 = 0$.
b) Solve the equation $2{x^4} + 3{x^2} - 2 = 0$ and hence find the coordinates of $A$ and $B$, giving your answers in an exact form.
پاسخ تشریحی :
تحلیل ویدئویی تست
منتظریم اولین نفر تحلیلش کنه!











