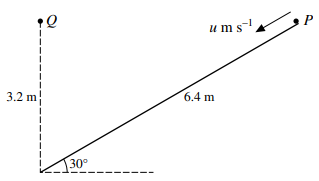
a) ${a_P} = g\sin {30^ \circ }$

$3.2 = {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}{\text{gt}}_q^2$

$\left[ {6.4 = u\left( {0.8} \right) + {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}5 \times {{\left( {0.8} \right)}^2}} \right]$

$u = 6$

b) [$v = 6 + 5 \times 0.8$ or ${v^2} = 36 + 2 \times 5 \times 6.4$]

Speed of $P$ is $10{\text{ }}m{s^{ - 1}}$

Alternative for Parts (a) and (b) when a is not used:

Part (a)

$3.2 = {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}{\text{gt}}_q^2$

For using $KE$ gain $ = PE{\text{ }}$ loss to obtain an equation in $u$ and $v$

$\left[ {{\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}\left( {{v^2} - {u^2}} \right) = 6.4g\sin {{30}^ \circ }} \right]$

For using $s = {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}\left( {u + v} \right)t$ to obtain a second equation in $u$ and $v$

$\left[ {6.4 = {\raise0.5ex\hbox{$\scriptstyle 1$}
\kern-0.1em/\kern-0.15em
\lower0.25ex\hbox{$\scriptstyle 2$}}\left( {u + v} \right) \times 0.8} \right]$

$u = 6$

Part (b)

Substitutes for $u$ to find $v$

Speed is $10{\text{ }}m{s^{ - 1}}$