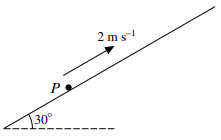
A particle $P$ of mass $0.2{\text{ }}kg$ is projected with velocity $2{\text{ }}m{\text{ }}{s^{ - 1}}$ upwards along a line of greatest slope on a plane inclined at ${30^ \circ }$ to the horizontal (see diagram). Air resistance of magnitude $0.5v{\text{ }}N$ opposes the motion of $P$, where $vm{\text{ }}{s^{ - 1}}$ is the velocity of $P$ at time $t\,s$ after projection. The coefficient of friction between $P$ and the plane is $\frac{1}{{2\surd 3}}$. The particle $P$ reaches a position of instantaneous rest when $t = T$.
a) Show that, while $P$ is moving up the plane, $\frac{{dv}}{{dt}} = - 2.5\left( {3 + v} \right)$.
b) Calculate $T$.
c) Calculate the speed of $P$ when $t = 2T$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...