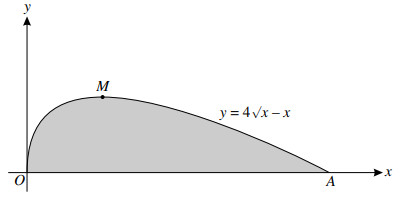
The diagram shows part of the curve $y = 4\surd x - x$. The curve has a maximum point at $M$ and meets the x-axis at $O$ and $A$.
a) Find the coordinates of $A$ and $M$.
b) Find the volume obtained when the shaded region is rotated through ${360^ \circ }$ about the x-axis, giving your answer in terms of $\pi $.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...