A tractor travels in a straight line from a point $A$ to a point $B$. The velocity of the tractor is $vm{\text{ }}{s^{ - 1}}$ at time $t\,s$ after leaving $A$.

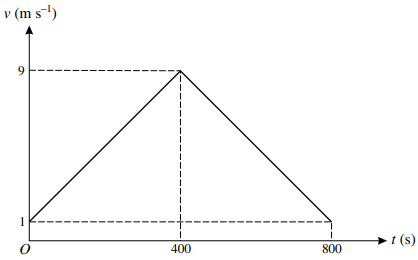
a) The diagram shows an approximate velocity-time graph for the motion of the tractor. The graph consists of two straight line segments. Use the graph to find an approximation for

(i) the distance $AB$,

(ii) the acceleration of the tractor for ${\text{0 \lt t \lt 400}}$ and for ${\text{400 \lt t \lt 800}}$.

b) The actual velocity of the tractor is given by $v = 0.04t - 0.00005{t^2}$ for $0 \leqslant t \leqslant 800$.

(i) Find the values of $t$ for which the actual acceleration of the tractor is given correctly by the approximate velocity-time graph in part (a).

For the interval $0 \leqslant t \leqslant 400$, the approximate velocity of the tractor in part (a) is denoted by ${v_1}{\text{ }}m{\text{ }}{s^{ - 1}}$.

(ii) Express ${v_1}$ in terms of $t$ and hence show that ${v_1} - v = 0.00005{\left( {t - 200} \right)^2} - 1$.

(iii) Deduce that $ - 1 \leqslant {v_1} - v \leqslant 1$.