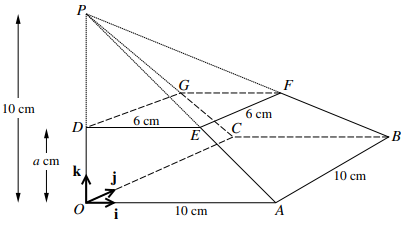
The diagram shows a pyramid $OABCP$ in which the horizontal base $OABC$ is a square of side $10{\text{ }}cm$ and the vertex $P$ is $10{\text{ }}cm$ vertically above $O$. The points $D$, $E$, $F4, $G4 lie on $OP$, $AP$, $BP$, $CP$ respectively and $DEFG$ is a horizontal square of side $6{\text{ }}cm$. The height of $DEFG$ above the base is $\alpha {\text{ }}cm$. Unit vectors i, j and k are parallel to $OA$, $OC$ and $OD$ respectively.
a) Show that $\alpha = 4$.
b) Express the vector $\overrightarrow {BG} $ in terms of $i$, $j$ and $k$.
c) Use a scalar product to find angle $GBA$.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...