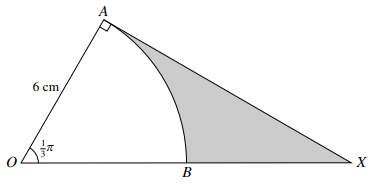
In the diagram, $AB$ is an arc of a circle, centre $O$ and radius $6{\text{ }}cm$, and angle $AOB = \frac{1}{3}\pi $ radians. The line $AX$ is a tangent to the circle at $A$, and $OBX$ is a straight line.
a) Show that the exact length of $AX$ is $6\surd 3{\text{ }}cm$.
Find, in terms of $\pi $ and $\surd 3$,
b) the area of the shaded region,
c) the perimeter of the shaded region.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...