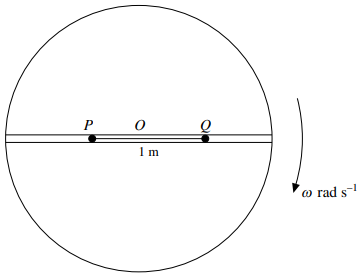
A narrow groove is cut along a diameter in the surface of a horizontal disc with centre $O$. Particles $P$ and $Q$, of masses $0.2{\text{ }}kg$ and $0.3{\text{ }}kg$ respectively, lie in the groove, and the coefficient of friction between each of the particles and the groove is $\mu $. The particles are attached to opposite ends of a light inextensible string of length $1{\text{ }}m$. The disc rotates with angular velocity $\omega {\text{ }}rad{\text{ }}{s^{ - 1}}$ about a vertical axis passing through $O$ and the particles move in horizontal circles (see diagram).

a) Given that $\mu  = 0.36$ and that both $P$ and $Q$ move in the same horizontal circle of radius $0.5{\text{ }}m$, calculate the greatest possible value of $\omega $ and the corresponding tension in the string.

b) Given instead that $\mu  = 0$ and that the tension in the string is $0.48{\text{ }}N$, calculate

(i) the radius of the circle in which $P$ moves and the radius of the circle in which $Q$ moves,

(ii) the speeds of the particles.