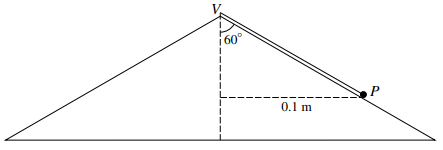
A particle $P$ of mass $0.5{\text{ }}kg$ is attached to the vertex $V$ of a fixed solid cone by a light inextensible string. $P$ lies on the smooth curved surface of the cone and moves in a horizontal circle of radius $0.1{\text{ }}m$ with centre on the axis of the cone. The cone has semi-vertical angle ${60^ \circ }$ (see diagram).
a) Calculate the speed of $P$, given that the tension in the string and the contact force between the cone and $P$ have the same magnitude.
b) Calculate the greatest angular speed at which $P$ can move on the surface of the cone.
پاسخ تشریحی :
تحلیل ویدئویی تست
تحلیل ویدئویی برای این تست ثبت نشده است!
محتواهای آموزشی مشابه
فایل های پاورپوینت، ویدئو، صوتی، متنی و ...
پرسش و پاسخ های مشابه
سوال کنید یا به سوالات دیگران پاسخ دهید ...