The distance travelled, in kilometres, by a Grippo brake pad before it needs to be replaced is modelled by $10000X$, where $X$ is a random variable having the probability density function

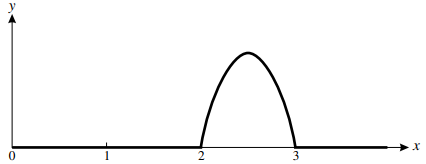
$f\left( x \right) = \left\{ \begin{gathered}   - k\left( {{x^2} - 5x + 6} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,2 \leqslant x \leqslant 3, \hfill \\  0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,otherwise. \hfill \\ \end{gathered}  \right.$

The graph of $y = f\left( x \right)$ is shown in the diagram.

a) Show that $k = 6$.

b) State the value of $E\left( X \right)$ and find $Var\left( X \right)$.

c) Sami fits four new Grippo brake pads on his car. Find the probability that at least one of these brake pads will need to be replaced after travelling less than $22000{\text{ }}km$.