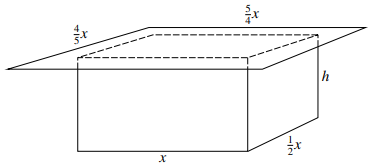
The diagram shows an open rectangular tank of height $h$ metres covered with a lid. The base of the tank has sides of length $x$ metres and $\frac{1}{2}x$ metres and the lid is a rectangle with sides of length $\frac{5}{4}x$ metres and $\frac{4}{5}x$ metres. When full the tank holds $4{\text{ }}{m^3}$ of water. The material from which the tank is made is of negligible thickness. The external surface area of the tank together with the area of the top of the lid is $A{\text{ }}{m^2}$.

a) Express $h$ in terms of $x$ and hence show that $A = \frac{3}{2}{x^2} + \frac{{24}}{x}$.

b) Given that $x$ can vary, find the value of $x$ for which $A$ is a minimum, showing clearly that $A$ is a minimum and not a maximum.