Three friends, Rick, Brenda and Ali, go to a football match but forget to say which entrance to the ground they will meet at. There are four entrances, $A$, $B$, $C$ and $D$. Each friend chooses an entrance independently.

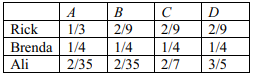
- The probability that Rick chooses entrance $A$ is $\frac{1}{3}$. The probabilities that he chooses entrances $B$, $C$ or $D$ are all equal.

- Brenda is equally likely to choose any of the four entrances.

- The probability that Ali chooses entrance $C$ is $\frac{2}{7}$ and the probability that he chooses entrance $D$ is $\frac{3}{5}$. The probabilities that he chooses the other two entrances are equal.

a) Find the probability that at least 2 friends will choose entrance $B$.

b) Find the probability that the three friends will all choose the same entrance.