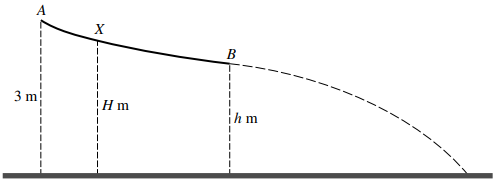
A smooth slide $AB$ is fixed so that its highest point $A$ is $3{\text{ }}m$ above horizontal ground. $B$ is $h{\text{ }}m$ above the ground. A particle $P$ of mass $0.2{\text{ }}kg$ is released from rest at a point on the slide. The particle moves down the slide and, after passing $B$, continues moving until it hits the ground (see diagram).

The speed of $P$ at $B$ is ${v_B}$ and the speed at which $P$ hits the ground is ${v_G}$.

a) In the case that $P$ is released at $A$, it is given that the kinetic energy of $P$ at $B$ is $1.6{\text{ }}J$. Find

(i) the value of $h$,

(ii) the kinetic energy of the particle immediately before it reaches the ground,

(iii) the ratio ${v_G}{\text{ }}:{\text{ }}{v_B}$.

b) In the case that $P$ is released at the point $X$ of the slide, which is $H{\text{ }}m$ above the ground (see diagram), it is given that ${v_G}{\text{ }}:{\text{ }}{v_B} = 2.55$. Find the value of $H$ correct to 2 significant figures.